Quantum Tanner code[1]

Description

Member of a family of QLDPC codes based on two compatible classical Tanner codes defined on a two-dimensional Cayley complex, a complex constructed from Cayley graphs of groups. For certain choices of codes and complex, the resulting codes have asymptotically good parameters. This construction has been generalized to Schreier graphs [2].

The underlying geometric complex of the code is a left-right Cayley complex \(\operatorname{Cay}_2(A,G,B)\), where \(G\) is a finite group and \(A=A^{-1}\), \(B=B^{-1}\) are two symmetric generating sets satisfying the total no-conjugacy condition: \(ag\ne gb\) for any \(g\in G\), \(a\in A\), and \(b\in B\). The vertices of the complex are group elements, i.e., \(V=G\). If necessary, the double cover of the graph should be taken so that the graph is bipartite, \(V=V_0\sqcup V_1\).

There are two types of edges in the resulting complex, \begin{align} \begin{split} E_A &= \{(g,ag): g\in G, a\in A\}\\ E_B &= \{(g,gb): g\in G, b\in B\}~. \end{split} \tag*{(1)}\end{align} The faces are squares defined by quadruples, \begin{align} Q = \{(g,ag,gb,agb): g\in G, a\in A, b\in B\}~. \tag*{(2)}\end{align} Two additional graphs can be obtained from \(\operatorname{Cay}_2(A,G,B)\) by taking the diagonals of the squares as edges, \(\mathcal G_0^\square = (V_0, Q)\) and \(\mathcal G_1^\square = (V_1, Q)\).

In the quantum Tanner construction, qubits are placed on the squares of the left-right Cayley complex. Two classical codes \(C_A\) and \(C_B\) of blocklengths \(|A|\) and \(|B|\), respectively, are chosen, yielding local codes \(C_0 = C_A\otimes C_B\) and \(C_1 = C_A^\perp\otimes C_B^\perp\). The quantum Tanner code is a CSS code defined by the classical Tanner codes \(C_Z = T(\mathcal G_0^\square, C_0^\perp)\) and \(C_X = T(\mathcal G_1^\square, C_1^\perp)\). The figure below depicts an example of a stabilizer generator.

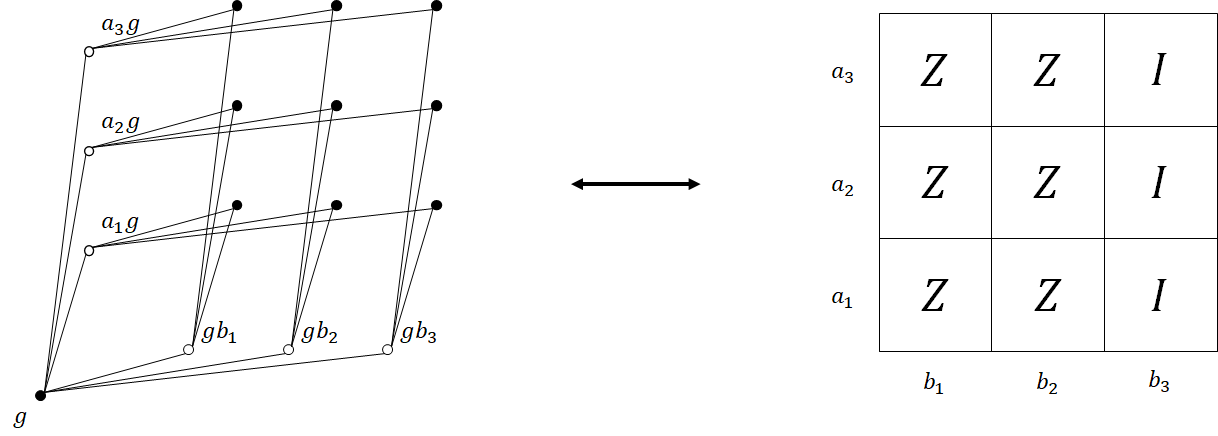
To achieve asymptotically good parameters, fixed classical local codes are chosen so that their dual tensor codes are sufficiently robust, and the left-right Cayley complexes are chosen to be sufficiently expanding. The family is defined using a family of groups \(G\) of increasing size but constant-size generating sets \(A\), \(B\).